roc

I'm trying to understand ROC curves. They look kinda like this:

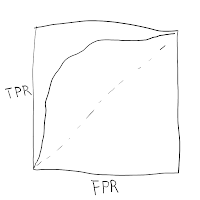
The TPR means True-Positive Rate. The FP means False-Positive Rate. I've said before that TP and FP confuse me. So let's start by trying to understand that. Here's a diagram to help me remember:

Ok, Wikipedia says TPR = "the fraction of true positives out of the positives". Seems like precision. But later it says "TPR is also known as sensitivity", where Wikipedia says sensitivity is the "probability of a positive test, given that the patient is ill." But that seems like recall. Alas. Which is it?

Poking around, I think that TPR is sensitivity, and FPR is related to specificity, i.e., it is 1 - specificity. What awful names. Why do people want names for related concepts that sound so much like each other?

Just to make sure I understand sensitivity and specificity: sensitivity is how accurate the test is on red dots, and specificity is how accurate the test is on grey dots.

So

TPR = sensitivity = recall.
FPR = 1 - specificity = 1 - "accuracy on grey dots" = "inaccuracy on grey dots"

Let's try to get some parallel construction:

TPR = probability of saying a red dot is red
FPR = probability of saying a grey dot is red

So both measures are probabilities of saying dots are red.

Fine. Now the ROC curve goes from the lower-left corner (0, 0), to the upper-right corner (1, 1). What does the lower-left corner mean? Low TPR and low FPR.. that means we're unlikely to say anything is red. That seems easy to achieve. Just never say anything is red. So that must be what happens when the threshold of our test is too high, such that nothing ever meets it.

The upper-right corner means high TPR and high FPR.. that means we're very likely to say things are red. That also seems easy to achieve. Just always say everything is red. So that must be what happens when the threshold of our test is too low, such that everything meets it.

So I suppose if we try different threshold values from low to high, we'll sortof draw a line from the upper-right corner to the lower-left corner. Perhaps it is easier to think of trying different threshold values from high to low so that we draw a curve going to the right.